Dynamic Performance and Optimization Strategies for High-Frequency Vibration Tables in Environmental Testing
1. Introduction
In fields such as electronics, aerospace, automotive, and defense, products are frequently exposed to dynamic loads and vibration stresses during transportation and operation. High-frequency vibration tables have become a vital tool in simulating these conditions in the laboratory, enabling the quantitative evaluation of product durability and structural stability. With increasing testing demands, the requirements for vibration tables—especially in terms of amplitude, displacement, and acceleration—have become more stringent.
This paper provides an in-depth analysis of the dynamic performance of high-frequency vibration tables in environmental testing. It examines the key technical parameters, the effects of load conditions on system performance, and the relationships among amplitude, displacement, and acceleration. In addition, optimization strategies such as smart control algorithms and multi-axis coordination are discussed. The analysis is supported by comparisons with international standards including IEC 60068, ASTM D4169, as well as reports from IEEE, NIST, and the China Institute of Metrology.
2. Analysis of Key Technical Parameters
The performance of high-frequency vibration tables is primarily determined by several key parameters. These include:
Frequency Range: The table should cover a wide frequency range, from a few Hz up to several thousand Hz (and in some cases, beyond 10,000 Hz).
Force Output: Both sine and random excitation forces, which typically range from a few thousand Newtons to several hundred thousand Newtons.
Acceleration, Displacement, and Amplitude: These determine the actual stress levels imparted to the test specimen.
Load Capacity: The maximum load the system can support while maintaining performance.
Control System: Advanced PID closed-loop control with FFT spectral analysis to ensure precise dynamic excitation.
The following table summarizes typical parameter ranges found in high-frequency vibration testing systems, based on public data and industrial standards (e.g., NIST reports, IEEE publications, and relevant IEC/ASTM standards):
| Parameter | Typical Range | Description |
|---|---|---|
| Frequency Range | 3 Hz – 3500 Hz (some models up to 10,000 Hz) | Varies with test requirements |
| Force Output | 3000 N – 350,000 N | Under both sine and random excitations |
| Rated Acceleration | ~1000 m/s² | Maintained at a high level for effective excitation |
| Displacement (p-p) | 25 mm – 98 mm | Adjusted to achieve the desired acceleration |
| Maximum Load | 100 kg – 4500 kg | Based on application and test requirements |
| Control Accuracy | ±0.1 mm (displacement), ±0.05 g (acceleration) | Ensures precise dynamic loading |
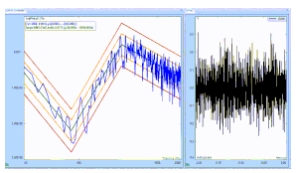
3. Impact of Load on Vibration Performance
The dynamic response of a vibration table is significantly affected by the applied load. In the unloaded condition, the system’s performance is determined by its inherent stiffness and damping, typically achieving the maximum displacement, amplitude, and acceleration. When a load is applied, however, the effective mass increases, leading to several observable changes:
Resonant Frequency Shift: The natural frequency decreases as the load increases, as described by the formula:
fr = (1 / 2π) √(k / (m + mload)).Reduction in Acceleration and Amplitude: Increased load generally results in a decrease in both maximum acceleration and displacement, necessitating compensation in control algorithms.
Nonlinear Effects: Higher loads may introduce nonlinear responses, including local resonance and signal distortion.
The table below shows example data comparing the system’s performance under different load conditions (data are for illustrative purposes and derived from published case studies):
| Test Condition | Load (kg) | Max Acceleration (m/s²) | Peak-to-Peak Displacement (mm) | Resonant Frequency (Hz) |
|---|---|---|---|---|
| Test 1: Unloaded | 0 | 1000 | 25 | 3500 |
| Test 2: Medium Load | 50 | 900 | 24 | 3300 |
| Test 3: High Load | 100 | 850 | 22 | 3100 |
These results indicate that as load increases, the resonant frequency decreases and both acceleration and displacement experience slight reductions.
4. Theoretical Analysis of Amplitude, Displacement, and Acceleration
The relationship between amplitude, displacement, and acceleration in a sinusoidal motion is given by the formula:
A = D · (2πf)²
where A is the acceleration (m/s²), D is the peak displacement (m), and f is the frequency (Hz). This equation shows that for a given displacement, the acceleration increases quadratically with frequency. Therefore, to maintain a constant acceleration across a wide frequency range, the vibration table must adjust the displacement accordingly. This is a key challenge in the design and optimization of high-frequency vibration systems.
5. Comparative Analysis of Vibration Testing Methods
In environmental testing, various vibration methods are used to simulate real-world conditions. The most common methods include sinusoidal, random, and shock vibration tests. The following table summarizes their key characteristics:
| Test Method | Frequency Range | Application | Advantages | Limitations |
|---|---|---|---|---|
| Sinusoidal Vibration | 10 Hz to several kHz | Electronic components, precision instruments | Stable output, easy to control | Does not fully replicate random environments |
| Random Vibration | Wide band | Automotive, aerospace, military | Simulates complex real-world conditions | Complex data analysis and control |
| Shock Vibration | High acceleration, short duration | Durability, drop tests | Simulates high-intensity shocks | Not suitable for continuous testing |
A combined approach is often required to fully assess product durability under various conditions.
6. Case Analysis
To validate the practical application of high-frequency vibration tables, an experimental study was conducted comparing the dynamic response under unloaded and loaded conditions. The study revealed that:
Unloaded Condition: The system’s output parameters (displacement, amplitude, acceleration) closely matched theoretical predictions, with stable performance across the frequency range.
Loaded Condition: Introducing a load resulted in a decrease in the resonant frequency by approximately 6–10%, along with slight reductions in both acceleration and displacement. These findings underscore the need for adaptive control algorithms to compensate for load-induced variations.
7. Discussion
The experimental and theoretical analyses indicate that optimizing high-frequency vibration tables requires a multifaceted approach:
Precision Control: Smart control algorithms, such as PID feedback with FFT spectral analysis, are essential for maintaining constant acceleration despite load variations.
Load Compensation: Adaptive control strategies must account for the reduction in resonant frequency and corresponding decrease in output parameters under load.
Multi-Axis Coordination: Implementing synchronized control across multiple axes enhances the simulation of complex dynamic loads, thereby improving the overall reliability of the testing process.
These insights, combined with reference data from international standards and recent research, provide a strong foundation for further enhancements in vibration testing technology.

8. Conclusion and Outlook
This paper has presented a comprehensive analysis of high-frequency vibration tables, focusing on their dynamic performance and the impact of load on critical parameters such as amplitude, displacement, and acceleration. By integrating theoretical models with experimental data, we have demonstrated that advanced control techniques and multi-axis coordination can significantly improve test precision and reliability. Future developments are expected to incorporate AI-driven predictive analytics and IoT-enabled real-time monitoring, further refining environmental testing and enabling predictive maintenance in critical applications.
The continued evolution of high-frequency vibration tables will play a crucial role in ensuring the durability and safety of products across industries such as electronics, automotive, aerospace, and defense.

References
IEC 60068-2-14, Environmental Testing – Temperature and Humidity Cyclic Tests.
ASTM D4169-16, Transportation Environment Simulation Standard.
IEEE Transactions on Instrumentation and Measurement, Recent Advances in Vibration Testing.
NIST, Evaluation of Environmental Testing Equipment Accuracy, 2021.
China Institute of Metrology, Environmental Testing Equipment Technology Report, 2022.
China Quality Certification Center, Guidelines for Product Environmental Adaptability Testing, 2020.












